Abstract
Zero-Knowledge Proofs (ZKPs) are among the most powerful cryptographic primitives in modern secure computation, enabling a prover to convince a verifier of the validity of a statement without revealing any additional information. The security and efficiency of ZKPs rely fundamentally on deep results from algebraic structures—sets, groups, rings, and fields. This article explores how these structures provide the foundation for ZKP protocols, ranging from classical sigma-protocols to advanced zk-SNARKs and zk-STARKs.
1. Algebraic Structures in Cryptography
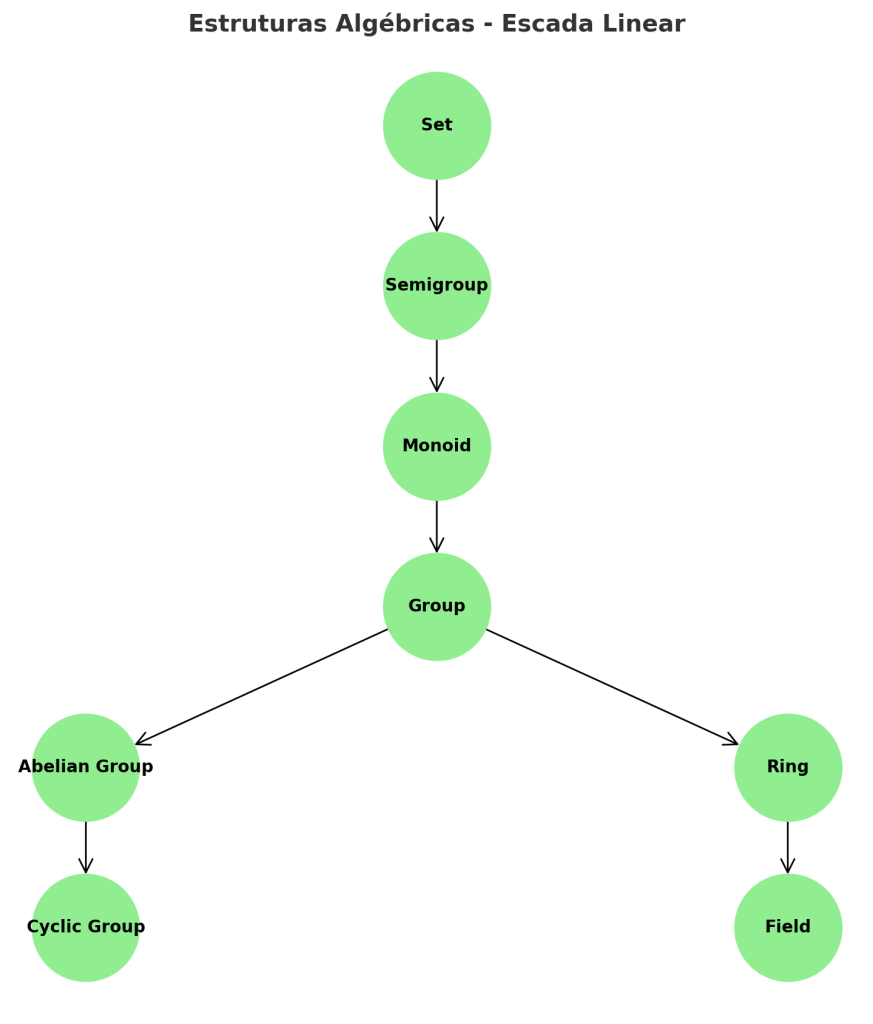
Cryptography, at its core, exploits hard problems within algebraic structures. Each layer of abstraction in algebra builds toward properties indispensable in ZKPs.
- Sets: The most primitive foundation, defining the universe of elements under consideration. For ZKPs, sets define the space of secrets (witnesses) and challenges.
- Semigroups and Monoids: Introduce closure and associativity under a binary operation. These properties guarantee that operations within ZKPs (e.g., repeated hashing, modular exponentiation) are consistently defined.
- Groups: Provide invertibility and well-defined algebraic manipulations. Most ZKP protocols, such as Schnorr’s protocol, are based on the hardness of the Discrete Logarithm Problem (DLP) in finite groups.
- Abelian Groups: Enforce commutativity, critical for efficiency in cryptographic proofs. Pairing-based cryptography, for instance, relies on bilinear maps defined over abelian groups.
- Cyclic Groups: Ensure that the entire group can be generated from a single element (the generator). This property underpins Diffie–Hellman hardness assumptions, which secure many sigma-protocols that form the building blocks of ZKPs.
- Rings: Introduce dual operations (addition and multiplication). Rings serve as the foundation for polynomial commitments, which are at the heart of modern zk-SNARK constructions.
- Fields: Provide multiplicative inverses (excluding zero), enabling division. Finite fields Fp\mathbb{F}_pFp or F2n\mathbb{F}_{2^n}F2n are indispensable in defining arithmetic circuits for zk-SNARKs and zk-STARKs, where computations are expressed as polynomials over finite fields.
2. ZKPs and Group-Theoretic Foundations
Early ZKPs, such as Schnorr’s identification scheme, directly leverage cyclic groups:
- Setup: Choose a large prime ppp and a generator ggg of a cyclic group Zp∗\mathbb{Z}_p^*Zp∗.
- Witness: Prover knows a secret xxx such that y=gxmod py = g^x \mod py=gxmodp.
- Protocol: By using random commitments and challenge-response interactions, the prover convinces the verifier of knowledge of xxx without revealing it.
The hardness of the Discrete Logarithm Problem (finding xxx given ggg and gxg^xgx) is what secures the zero-knowledge property.
3. Polynomial Algebra and Modern ZKPs
Modern ZKP systems, such as zk-SNARKs and zk-STARKs, shift from discrete logarithms to algebraic constraint systems:
- Arithmetic Circuits: Arbitrary computations are expressed as circuits over a finite field Fp\mathbb{F}_pFp.
- Each wire carries an element of Fp\mathbb{F}_pFp.
- Each gate enforces addition or multiplication constraints.
- Quadratic Arithmetic Programs (QAPs): Encode circuit satisfiability into polynomial equations.
- The prover demonstrates knowledge of a solution (witness vector) that satisfies these polynomials.
- This reduces computational integrity to polynomial identities over fields.
- Polynomial Commitments: Allow the prover to commit to polynomials while later opening evaluations at specific points.
- Implemented via algebraic tools such as KZG commitments (pairing-based, requiring cyclic groups with bilinear maps).
- Or via FRI (Fast Reed-Solomon Interactive Oracle Proofs) in STARKs, using properties of fields and error-correcting codes.
4. Why Algebraic Structures Are Indispensable
- Soundness: Relies on group hardness assumptions (e.g., discrete log, elliptic curve assumptions).
- Zero-Knowledge: Achieved via randomness and masking within algebraic groups, ensuring simulatable transcripts.
- Efficiency: Rings and fields allow complex computations to be reduced to polynomial equations, optimized for succinct verification.
- Post-Quantum Security: Moving to lattice-based assumptions involves working in algebraic structures such as modules over rings (e.g., Ring-LWE), which are being actively researched for post-quantum ZKPs.
5. Conclusion
Algebraic structures form the mathematical DNA of Zero-Knowledge Proofs. From the simplicity of cyclic groups in Schnorr’s protocol to the sophisticated use of finite fields and polynomial rings in zk-SNARKs and zk-STARKs, every step of ZKP evolution has been powered by algebra. Understanding sets, groups, rings, and fields is not merely academic—it is the key to designing secure, efficient, and future-proof privacy-preserving protocols.